Bern lakes - example canton#
Summary and analysis of observations of trash density: objects related to tobacco and food and drink found in lakes. Report number: Bern lakes- example canton lake 2020-01-01 2021-05-31
Proof of concept: llm assissted reporting grid forecasting example
Executive Summary#
The report on the Bern lakes example canton presents findings from 13 cities, including Biel/Bienne, Vinelz, and Thun, alongside three lakes: Bielersee, Brienzersee, and Thunersee. The sampling took place between January 26, 2020, and April 8, 2021, in the Aare survey area, resulting in 74 samples collected. The analysis yielded an average density of 0.69 pcs/m, with a maximum density of 3.88 pcs/m and a standard deviation of 0.89. A total of 2,128 objects were identified, predominantly consisting of plastic materials. The most frequently found items were cigarette filters and food wrappers, with fail rates indicating that they were present in the majority of samples.
Sampling stratification is defined as the process of dividing the survey area into segments based on specific characteristics. In this study, land-use features such as buildings, wetlands, and forests were considered, revealing that trash density varies significantly according to these characteristics. The analysis indicated a correlation between higher trash densities and areas with more buildings, as well as mixed land-use environments. Specifically, locations with buildings occupying 0-20% of the buffer exhibited an average trash density of 0.59 pcs/m, while those with forests at 20-40% showed 0.88 pcs/m, highlighting the influence of land-use distribution on litter accumulation.
The report employed linear and ensemble regression methods to analyze the data. The Gradient Boosting Regression model demonstrated the highest R² of 0.43 and a mean squared error (MSE) of 0.36, suggesting a moderate level of reliability in its predictions. The feature importance analysis indicated that buildings and streets were significant in predicting trash density, with the highest permutation importance assigned to buildings at 0.137. These results suggest that while the model explains a portion of variance in trash density, there are likely other factors that could further influence predictions.
Grid approximation was utilized as a statistical modeling technique to estimate the likelihood of trash density observations exceeding specified thresholds. In this case, the prior data was analyzed in terms of in-boundary and out-boundary conditions, revealing that the in-boundary average was lower (0.82 pcs/m) than the observed average (0.69 pcs/m), while the out-boundary average (1.09 pcs/m) was higher. This indicates an anticipated increase in trash density in out-boundary areas, contrasting with a potentially lower density in in-boundary regions.
Sample results#
The report on the Bern lakes example canton includes observations from 13 cities: Biel/Bienne, Vinelz, Brienz (BE), Spiez, Lüscherz, Nidau, Gals, Unterseen, Erlach, Thun, Beatenberg, Ligerz, and Bönigen. There are three lakes included in the analysis: Bielersee, Brienzersee, and Thunersee.
The sampling took place from January 26, 2020, to April 8, 2021, in the survey area named Aare. A total of 74 samples were collected, yielding an average density of 0.69 pcs/m (objects per meter), a median of 0.35 pcs/m, a maximum of 3.88 pcs/m, and a standard deviation of 0.89. The total number of objects identified across all locations was 2128.
The most common objects found by greatest quantity were:
Cigarette filters - Fail rate: 83.78%, Percent of total: 73.45%, pcs/m: 0.48, Total quantity: 1563.
Food wrappers; candy, snacks - Fail rate: 82.43%, Percent of total: 26.55%, pcs/m: 0.22, Total quantity: 565.
The material composition of the identified objects was entirely plastic, representing 100% of the total.
Sample results frequently asked questions
Frequently asked questions
1. What were the ten most common items found?
The top two common items identified were:
Cigarette filters - Fail rate: 83.78%, Percent of total: 73.45%.
Food wrappers; candy, snacks - Fail rate: 82.43%, Percent of total: 26.55%.
(Note: Only two items were provided in the report with a fail rate above 0.5.)
2. Are these objects found on European beaches? If so, is there any data on how many per 100 m of beach?
Yes, these objects are commonly found on European beaches. According to the OSPAR results from 2021, cigarette butts were reported at a density of approximately 40 items per 100 meters of beach. For more detailed information, you can refer to their official report at OSPAR 2021 Beach Litter Results.
3. What are possible sources of these specific objects?
Possible sources of these objects include recreational activities (e.g., picnicking, smoking), littering, public events, and inadequate waste management systems. Cigarette filters are often discarded carelessly by smokers, while food wrappers originate from snacks consumed in public spaces.
4. Which three cities had the highest average pcs/m? Which three had the lowest?
The three cities with the highest average pcs/m were:
Biel/Bienne - 1.79 pcs/m.
Bönigen - 1.25 pcs/m.
Ligerz - 1.55 pcs/m.
The three cities with the lowest average pcs/m were:
Lüscherz - 0.06 pcs/m.
Spiez - 0.08 pcs/m.
Thun - 0.31 pcs/m.
| pcs/m | buildings | forest | undefined | streets | public-services | recreation | |
|---|---|---|---|---|---|---|---|
| cluster | |||||||
| 0 | 1,54 | 0,14 | 0,31 | 0,30 | 0,27 | 0,19 | 0,01 |
| 1 | 0,79 | 0,31 | 0,11 | 0,54 | 0,50 | 0,06 | 0,03 |
| 2 | 0,35 | 0,68 | 0,15 | 0,15 | 0,25 | 0,04 | 0,00 |
| 3 | 0,52 | 0,17 | 0,56 | 0,13 | 0,10 | 0,04 | 0,00 |
Sampling stratification#
Sampling stratification refers to the process of dividing the survey area into different segments based on specific characteristics, such as land use. In the context of the Bern lakes survey, the stratification considers the proportion of the surrounding buffer zone that is dedicated to various land-use features, which helps ensure that samples collected are representative of the environmental conditions present. The land-use features include buildings, wetlands, forests, public services, recreation areas, and others. The results from the survey can then be analyzed in relation to these stratified characteristics, allowing for a better understanding of how different land uses correlate with trash density.
In the sampling stratification and trash density table, the highest pieces of trash per meter (pcs/m) values were found in the ‘forest’ and ‘buildings’ categories. For example, in areas where buildings occupied 0-20% of the buffer, the average trash density was 0.59 pcs/m, with 31.1% of all samples taken from this land-use classification. Conversely, in areas where forests occupied 20-40% of the buffer, the average trash density was 0.88 pcs/m, with 66.2% of samples taken from this classification. These values indicate the varying levels of trash density according to the land-use features surrounding the surveyed locations.
| Proportion of samples collected | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| buildings | wetlands | forest | public-services | recreation | undefined | streets | vineyards | orchards | |
| proportion of buffer | |||||||||
| 0-20% | 31.1% | 100.0% | 24.3% | 100.0% | 100.0% | 35.1% | 44.6% | 100.0% | 100.0% |
| 20-40% | 37.8% | none | 66.2% | none | none | 8.1% | 8.1% | none | none |
| 40-60% | 21.6% | none | 9.5% | none | none | 56.8% | 18.9% | none | none |
| 60-80% | 6.8% | none | none | none | none | none | 20.3% | none | none |
| 80-100% | 2.7% | none | none | none | none | none | 8.1% | none | none |
| Pieces of trash per meter | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| buildings | wetlands | forest | public-services | recreation | undefined | streets | vineyards | orchards | |
| proportion of buffer | |||||||||
| 0-20% | 0,59 | 0,69 | 0,34 | 0,69 | 0,69 | 1,12 | 0,34 | 0,69 | 0,69 |
| 20-40% | 0,22 | none | 0,88 | none | none | 1,15 | 0,65 | none | none |
| 40-60% | 1,79 | none | 0,23 | none | none | 0,36 | 0,33 | none | none |
| 60-80% | 0,40 | none | none | none | none | none | 1,90 | none | none |
| 80-100% | 0,31 | none | none | none | none | none | 0,47 | none | none |
Sampling stratification frequently asked questions
Frequently asked questions
1. What does the sampling stratification table tell us?
The sampling stratification table provides insights into the distribution of trash density across different land-use features surrounding the surveyed locations. For instance, the highest value in the buildings column is 0.59 pcs/m, which corresponds to areas where buildings occupy 0-20% of the buffer zone, and 31.1% of the samples were taken from this category. In contrast, the highest value in the undefined column is 1.12 pcs/m, with 35.1% of the samples collected from areas that fall within the 0-20% buffer zone. These values reflect the concentration of litter in varying land-use contexts, indicating that different environments may experience different levels of trash density.
2. How can the information in the sampling stratification and trash density table help identify areas of concern?
The information in the sampling stratification and trash density table can help identify areas of concern by highlighting which land-use features are associated with higher levels of trash density. For example, if certain areas, such as those with more buildings or undefined land uses, exhibit significantly higher trash densities, it may indicate a need for targeted waste management strategies or cleanup efforts in those regions. The data enables stakeholders to prioritize areas where litter is most prevalent and may pose risks to the environment and public health.
3. Under what land-use conditions would a surveyor expect to find the most trash?
A surveyor would expect to find the most trash in areas where buildings are prevalent and in certain undefined land-use contexts. For example, in locations where buildings occupy 40-60% of the buffer, the average trash density is 1.79 pcs/m. Additionally, in areas where undefined land use occupies 0-20% of the buffer, the average trash density is 1.12 pcs/m. These figures suggest that higher concentrations of buildings and undefined land uses correlate with increased litter levels.
4. Given the results in the sampling stratification table, were these surveys collected in mostly urban environments or forested?
The surveys do not meet the criteria to be classified strictly as urban or rural. The sum of the proportions of samples for buildings in the rows 60-80% and 80-100% is 0.0%, while the sum for forests in these same rows is also 0.0%. Therefore, both categories are below the required 50% threshold. The highest proportion of samples was collected from areas where buildings occupy 0-20% of the buffer (31.1%) and forests occupy 20-40% of the buffer (66.2%), indicating a mixed land-use environment.
Linear and ensemble methods#
Cluster analysis, specifically K-Means, is a method used to partition a dataset into distinct groups or clusters based on the similarity of the data points. The algorithm works by initially selecting a predefined number of clusters (k) and then iteratively assigning data points to the nearest cluster center while updating the cluster centers based on the data points assigned to them until convergence is reached.
The cluster that had the highest average pcs/m (objects per meter of beach) was Cluster 0, which had a density of 1.55 pcs/m. The composition of this cluster in terms of land use features was as follows: buildings occupied 0.14 (14%) of the buffer zone, forest occupied 0.31 (31.0%), and undefined land use occupied 0.30 (30.0%) of the buffer.
Linear regression is a statistical method used to model the relationship between a dependent variable and one or more independent variables by fitting a linear equation to observed data. The basic assumptions of linear regression include linearity (the relationship between the independent and dependent variable is linear), independence (observations are independent of each other), homoscedasticity (constant variance of errors), and normality (the residuals of the model are normally distributed).
Ensemble regression methods, such as Random Forest and Gradient Boosting, combine multiple individual models to produce a more accurate and robust prediction. These methods also have assumptions, including the need for the individual models to be diverse and the feature set being relevant to the target variable.
The regression analysis conducted revealed that the model with the highest R² was the Gradient Boosting Regression model, which had an R² of 0.43 and a mean squared error (MSE) of 0.36. Given this R² and MSE, the predictions made using this model would indicate a moderate level of reliability, with the model explaining approximately 43.2% of the variance in the data, while the MSE suggests that there is a reasonable amount of error in the predictions.
Linear methods frequently asked questions
Frequently asked questions
What were the r² and MSE of each test?
The following are the R² and MSE results from the regression analysis conducted:
Linear Regression: R² = 0.27, MSE = 0.46
Random Forest Regression: R² = 0.25, MSE = 0.47
Gradient Boosting Regression: R² = 0.43, MSE = 0.36
Theil-Sen Regressor: R² = 0.36, MSE = 0.41
Bagging: Gradient Boosting Regression: R² = 0.43, MSE = 0.36
Voting: R² = 0.37, MSE = 0.40
Given the r² and MSE of the different methods employed, how reliable do you think predictions would be based on these models?
Based on the R² and MSE values, predictions would vary in reliability. The Gradient Boosting Regression model, with the highest R² of 0.43 and MSE of 0.36, suggests that predictions using this model are moderately reliable, explaining around 43.2% of the variance in the data. Other models show lower R² values, indicating less explained variance and potentially less reliable predictions.
Can any conclusions be drawn from these results?
Yes, conclusions can be drawn that the Gradient Boosting Regression model is the most effective among those tested for predicting the target variable, as indicated by its higher R². However, the relatively low R² values across all models suggest that there may be other factors influencing the target variable that are not included in the model.
According to the cluster analysis, what is the cluster that has the greatest average pcs/m? What is the distribution of land use values within the cluster?
The cluster that has the greatest average pcs/m is Cluster 0, with a density of 1.55 pcs/m. The distribution of land use values within this cluster is as follows: buildings occupy 14% of the buffer, forest occupies 31.0%, and undefined land use occupies 30.0% of the buffer zone.
Forecasts and methods#
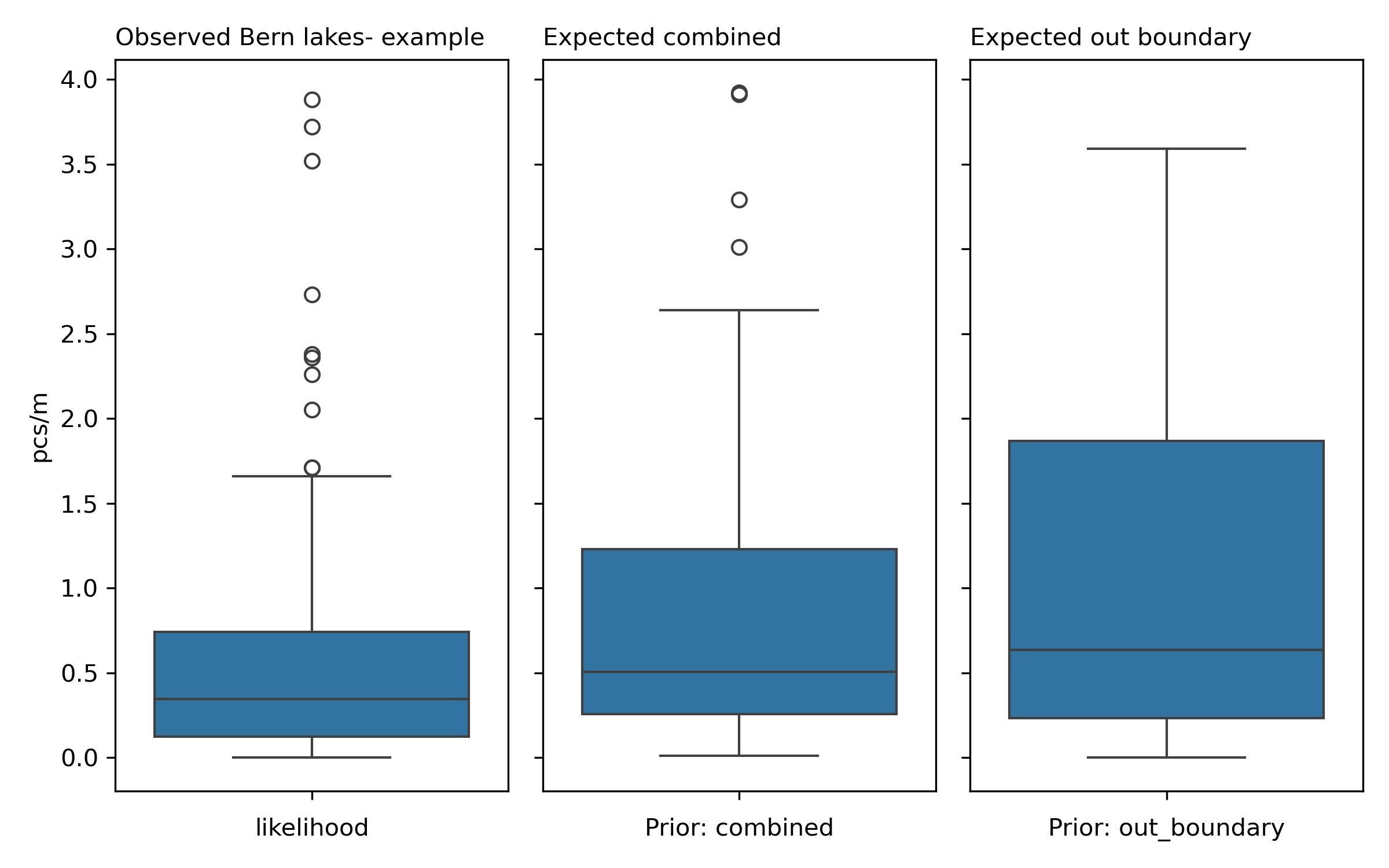
A grid approximation is a statistical modeling technique that estimates the likelihood of a particular survey result exceeding a specified threshold by analyzing prior observations and new data from the location of interest. This process utilizes an inference table, which organizes various probabilities associated with different outcomes based on prior and likelihood distributions. Inference tables typically consist of prior probabilities, likelihoods, and posterior probabilities, where the prior represents previous knowledge about the data, and the posterior is the updated probability after considering new evidence.
In the context of the report, the prior data utilized for grid approximations are categorized as follows:
In-boundary prior: Average pcs/m = 0.82, Median pcs/m = 0.51
Out-boundary prior: Average pcs/m = 1.09, Median pcs/m = 0.64
The posterior distributions derived from the grid approximation help estimate the conditional probabilities of observed results. By comparing the average posterior values to the observed results in pcs/m, we can see that the in-boundary average (0.82) is lower than the observed average (0.69), while the out-boundary average (1.09) is higher than the observed average. This indicates that there may be a tendency for an increase in trash density in the out-boundary areas, while in-boundary areas show a lower average than what was observed.
If a person takes one sample, the likelihood of observing an increase or decrease from the observed results is determined by the variability and the sample size. Given the standard deviation of the observed results (0.89 pcs/m), one sample could yield a result that is significantly different from the observed average. However, if two samples are taken, the likelihood of observing a mean closer to the true average increases, and the effects of variance diminish, thereby increasing the reliability of the observation.
Grid approximation frequently asked questions
Frequently asked questions
1. Why is grid approximation a reasonable modeling technique given the data?
Grid approximation is an appropriate modeling technique in this context due to the observed data’s skewness, indicated by the difference between the mean (0.69) and the median (0.35) from the summary statistics. The mean is significantly higher than the median, suggesting that the data may not be normally distributed. If the data were normally distributed, predictions would typically be centered around the mean, but the skewness implies that we must consider a wider range of potential outcomes, particularly in predicting the likelihood of future observations.
2. Do you have an example of other fields or domains that use grid approximation or Bayesian methods?
Grid approximation and Bayesian methods are commonly utilized in fields such as environmental science (for modeling pollution levels), finance (for risk assessment), and epidemiology (for disease outbreak predictions).
3. If the data is normally distributed, would the predictions from the grid approximation and the predictions from the normal distribution be different? If so, in what way?
Yes, if the data were normally distributed, predictions from the grid approximation would likely converge towards the mean, leading to a narrower range of expected outcomes. In contrast, a normal distribution would provide a symmetric view of the likelihood of observations, thus producing different estimates when compared to the grid approximation, which is informed by both prior distributions and observed evidence.
4. What is the difference between grid approximation and linear or ensemble regression?
Grid approximation is a probabilistic modeling approach that focuses on estimating the likelihood of different outcomes based on prior knowledge and new evidence, while linear regression is a deterministic method that predicts outcomes based on a relationship between dependent and independent variables. Ensemble regression combines multiple models to improve prediction accuracy, whereas grid approximation does not inherently include multiple modeling approaches but rather focuses on posterior probability estimation from prior data.
5. With which posterior do we expect to find most? The least?
Based on the averages of the posteriors, we would expect to find most in the out-boundary posterior (average pcs/m = 1.09) due to its higher value compared to the observed average. Conversely, we expect to find the least in the in-boundary posterior (average pcs/m = 0.82), which is lower than the observed average.
6. If the in-boundary grid approximation predicts an increase or decrease, what does that say about the other samples from within the boundary?
If the in-boundary grid approximation predicts an increase, it implies that elevated trash densities have likely been observed in other locations within the same geographic boundary. The prior reflects similar locations, and a weighted average with the likelihood suggests that other samples are likely indicating higher values as well.
7. If the out-boundary grid approximation predicts an increase or decrease, what does that say about the other samples from outside of the boundary?
If the out-boundary grid approximation predicts an increase, it suggests that locations outside the geographic boundary have shown elevated trash densities compared to the likelihood of the observations. The prior for out-boundary samples indicates that there may be higher densities elsewhere, which influences the posterior distribution.
8. How different are the expected results from the observed results? Should an increase or decrease be expected?
The expected results from the in-boundary posterior (average pcs/m = 0.82) and out-boundary posterior (average pcs/m = 1.09) differ from the observed average (0.69) in significant ways. The in-boundary posterior indicates a potential increase in trash density compared to the observed results, while the out-boundary posterior suggests a higher density than observed. Given the observed standard deviation (0.89 pcs/m), it is plausible to expect variability in future observations, but overall, the data suggests an increase in trash density, particularly in out-boundary areas, could be expected.
Consolidated results : city, survey area#
| city | quantity | pcs/m |
|---|---|---|
| Beatenberg | 29 | 0,67 |
| Biel/Bienne | 1'001 | 1,79 |
| Brienz (BE) | 68 | 0,46 |
| Bönigen | 106 | 1,25 |
| Erlach | 28 | 0,49 |
| Gals | 8 | 0,21 |
| Ligerz | 24 | 1,54 |
| Lüscherz | 17 | 0,06 |
| Nidau | 15 | 0,60 |
| Spiez | 50 | 0,08 |
| Thun | 65 | 0,31 |
| Unterseen | 658 | 0,69 |
| Vinelz | 59 | 0,33 |
| parent_boundary | quantity | pcs/m |
|---|---|---|
| aare | 2'128 | 0,69 |
Inventory#
| quantity | pcs/m | % of total | sample_id | fail rate | object |
|---|---|---|---|---|---|
| 1'563 | 0,48 | 0,73 | 74 | 0,84 | Cigarette filters |
| 565 | 0,22 | 0,27 | 74 | 0,82 | Food wrappers; candy, snacks |